[ML Research]Activation Function
업데이트:
앞서 DSC Yonsei 임성수 님께서 작성해 주신 Logistic Regression post에서 input과 가중치의 선형결합을 sigmoid 함수에 넣어서 output으로 이진분류를 하는 것을 배웠습니다.
또한 저의 지난 post인 ANN(Artificial Neural Network)에서는 MLP에서 각 노드들이 선형결합을 하고 activation function을 통해 노드의 input을 일종의 신호로 반환한다는 것을 배웠습니다.
따라서 이러한 post를 선험적으로 보는 것이 이번 포스트를 이해하는데 많은 도움이 될 수 있을 것이라고 생각합니다.
개요
우선 Activation Function과 같은 경우에는 MLP에서 input을 일종의 신호로 변환할 때 중요하게 작용합니다.
핵심적인 것으로는 숫자가 너무 크지 않아야 하고, 오차의 역전파 시 미분이 용이해야한다는 점이 중요합니다.
그 종류로는 다음고 같은 것들이 있고 이것들을 하나하나 따져가며 살펴봅시다.
- Sigmoid function
- ReLU function
- Leaky ReLU function
- GeLU function
Sigmoid function
우선 대표적으로는 앞서 언급한 logistic regression에서 사용되는 Sigmoid function 입니다.
시그모이드 함수는 그 그래프를 그렸을 때, 아래와 같이 0과 1사이의 값을 갖고 있고 $\phi(z) = {1 \over e^z}$의 식으로 표현됩니다.

그런데 이러한 sigmoid function의 식을 보면 하나 특이한 점이 있습니다. exponential function을 합성한 형태로 미분할 경우 너무 간단하 꼴이 도출된다는 점입니다.
따라서, MLP의 특성상 backpropagation을 써야하고, 그렇기 때문에 미분이 너무 복잡하면 안되고 이러한 관점에서 볼 때 활성화 함수로 용이합니다.
한 가지 단점은 layer가 더 깊이 쌓이는 모델에 backpropagation의 과정에 gradient가 0으로 수렴하는 gradient vanishing 문제가 발생한다는 것입니다..
이러한 단점은 너무나도 치명적이라서 최근 모델의 복잡도가 높아지는 추세에서는 잘 쓰이지 않는 편입니다.
ReLU function
ReLU는 앞서 언급한 시그모이드 함수의 단점인 gradient vanishing 문제를 성공적으로 잘 해결한 활성화 함수입니다.
많은 논문들에서 해당 활성화 함수를 사용하고 있기도 합니다.
이 함수를 식으로 표현하면 $y = max(0, x)$이고 그림으로 표현하면 아래와 같습니다. 즉, x가 음수일 경우 0의 함수값을 갖고, x가 양수인 경우는 1차식의 형태를 갖습니다.
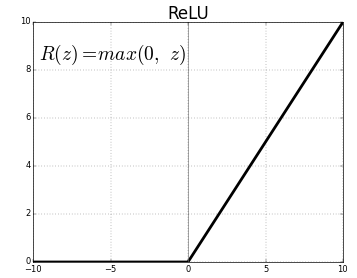
그러나 gradient vanishing 문제를 해결했음에도 불구하고 다른 문제가 생기게 되었습니다.
x의 음수부에서 완전히 0의 값을 갖는 것으로 인해. Dying ReLU라는 현상이 발생하는 것입니다.
Leaky ReLU
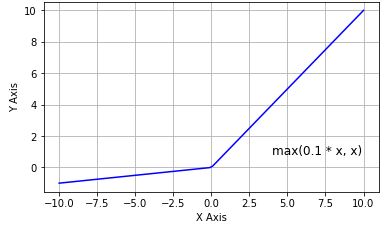
따라서 이러한 Dying ReLU의 단점을 보완하기 위해 탄생한 것이 바로 Leaky ReLU 함수 입니다. 이것은 x가 음수부에서 0이 되는 것을 보완하기 위해 아주 작은 음수의 값을 갖도록 식을 아래와 같이 조정하였습니다.
\[y = max(0.01x, x)\]그림으로 보면 아래와 같습니다.
GeLU
GeLU 함수는 수학적 이론이 많이 포함된 함수입니다. Google에서 Transformer 모델을 만들 당시 해당 Activation function을 사용한 뒤로, 많은 사랑을 받고 있는 함수라고 할 수 있습니다.
GeLU는 dropout과 ReLU함수에서 영향을 받아서 만들어졌다고 합니다. 따라서 bernoulli distribution function으로 dropout을 대체하였고, input과 결합하여 아래의 식으로 나타낼 수 있습니다.
\[y = x \\Phi(x) = x0.5\[1+erf({x \\over \\sqrt(2)})\]\]여기서 erf는 error function이고 이를 근사하여 Sigmoid Linear Unit으로 나타낼 수 있습니다. 그럼 식이 다음과 같고, $x\sigma$ 논문의 저자들은 이러한 근사의 방법이 계산이 간편하여 유용하다고 하고 있습니다.
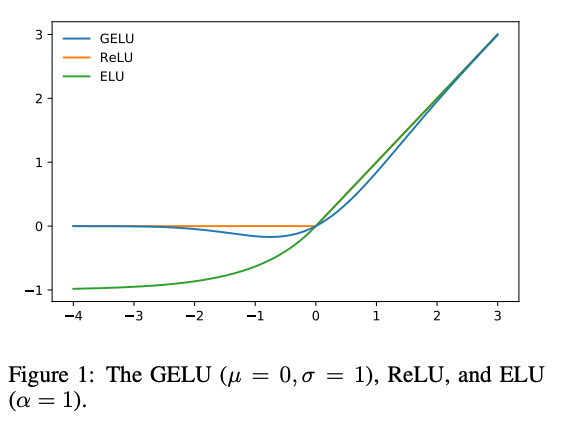
한편, GeLU는 분포의 함수이기에 평균과 분산에 따라 함수가 다양한데, 대체로 평균은 0 분산은 1인 함수를 사용한다고 합니다.
그림은 아래와 같습니다.
구현
Libraries & Load Data
import tensorflow as tf
from tensorflow import keras
# 헬퍼(helper) 라이브러리를 임포트합니다
import numpy as np
import matplotlib.pyplot as plt
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
Preprocess
train_images = train_images / 255.0
test_images = test_images / 255.0
ReLU model
relu = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
relu.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
relu = relu.fit(train_images, train_labels, epochs=5)
GeLU model
gelu = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='gelu'),
keras.layers.Dense(10, activation='softmax')
])
gelu.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
gelu = gelu.fit(train_images, train_labels, epochs =5)
Sigmoid model
sigmoid = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='sigmoid'),
keras.layers.Dense(10, activation='softmax')
])
sigmoid.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
sigmoid = sigmoid.fit(train_images, train_labels, epochs =5)
Leaky ReLU model
leaky = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation=tf.keras.layers.LeakyReLU()),
keras.layers.Dense(10, activation='softmax')
])
leaky.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
leaky = leaky.fit(train_images, train_labels, epochs =5)
Visualization
def plot_graphs(relu, gelu, sigmoid, leaky):
# loss
plt.plot(relu.history['loss'])
plt.plot(gelu.history['loss'])
plt.plot(sigmoid.history['loss'])
plt.plot(leaky.history['loss'])
plt.xlabel("Epochs")
plt.legend(['relu_loss', 'gelu_loss', 'sigmoid_loss', 'leaky_relu_loss'])
plt.show()
plot_graphs(relu, gelu, sigmoid, leaky)


